摘要  正确讲授微分是数学界还未解决的问题，本文首先简述了《浅谈现行微积分原理的错误》和《略论作为微积分原理的完善的实变函数》发表后在学界的反应；其次，指出用矩阵定义微分的做法仍然是错误的；最后，给出了正确讲授微分的方法。

0、引言

2015年底《前沿科学》发表拙文《浅谈现行微积分原理的错误》，2016年3月北京大学数学文化研究会和中国人民大学青年数学研究学会等联合发起了“重新审视微积分原理”系列学术报告会，并于4月底和5月初邀请林群院士、笔者和张景中院士在人大和北大等几所高校做系列学术报告。让人匪夷所思的是，就这么一场学术报告，竟有一所高校出尔反尔地单方把它“撤销”了,不仅如此，海外政治势力出动了在该校的未来到该国留学的学生群体，校方出动了团委及所属社团，还有保卫部门、维稳队伍、校卫队等，以共同阻止已对外发出参会海报的报告会的进行。作为惩处，相关领导和团委还取缔了该校的数学社团。还有，当时主持工作的领导还组织了有数学院士参与的数学教授队伍，以反击拙文《浅谈现行微积分原理的错误》。折腾了半天，最后的结论是“这个工科男在数学上捡了个天大的洋便宜。”

封杀当然不能客气，否则，还能再拿国际上的基金吗？有趣的是，2017年开学，在北京大学某微积分课堂上，微分定义的讲法被统一到陈天权的用矩阵定义的讲法上，而不再采用其它讲法。我们应该怎样理解这种“莫名其妙”的行径呢？

还有，有的数学教师说：“即使现行微积分原理有错误，也不能说明现行微积分原理是错的，因为，到了实变函数理论那里所有问题都解决了。”事实是这样吗？2016年底，《前沿科学》又发表了笔者的《略论作为微积分原理的完善的实变函数》，笔者在这里指明了现行实数理论、测度理论、无穷集合理论等诸个领域中的根本性错误。

用矩阵，改变的只是表达方式，并没有改变自柯西以来的错误机理。而数学工作者，没有理由再讲授错误的理论。因为，讲错了，是能力问题；坚持错误，是道德问题。

牛顿和莱布尼兹一生也没能建立起能自圆其说的微积分原理，柯西建立起来了，可是，一直就是错误的。发现这些问题难，敢于确信自己的发现真比登天还难。而解决问题就更难，可解决了之后，问题简单得让人不敢相信。诚如数学家张景中院士所说：“任何一个创造，在实现之前，都是困难的。因为人们是在无知中摸索。摸到之后，就成简单的了。”

给出并让数学教师接受新的微分讲授方法，还得从现行微积分原理说起。

1. 极限论与现行微积分原理的错误

谙熟数学史的学者都知道，现行微积分原理，就是在无奈时拼接了一点儿莱布尼兹的微分的极限化的牛顿的“微积分原理”。为什么一定要“拼接一点儿莱布尼兹的微分”呢？就是为了解释以微分方程求解方法为主的方方面面问题，否则，还成其为原理吗？要解决这些问题，就得有“微商”这一无法规避的东西，拼接莱布尼兹的微分的目的就在于此。

柯西为什么不以莱布尼兹的微积分原理为基础再通过拼接一点牛顿或者别人的什么东西形成微积分原理呢？因为柯西根本没有这样的数学功夫。莱布尼兹先定义微分的微积分原理是最简明易懂的，可是，他的微分说不清楚。莱布尼兹引进“dx表示两相邻x的差值。”那么，这“两相邻x”有多近呢？答曰：要多近就有多近。这个“要多近就有多近”就是问题。

其实，这个问题不能由莱布尼兹负责，问题出在数学的数-形模型上。这种问题无论是单独从数的模型上还是从几何模型上都不容易发现，一旦把两者联合起来——从解析几何角度出发，就一目了然了。下面，我们以现行解析几何中的圆与正多边形的关系为例加以说明。在现行解析几何中，到定点的距离为定长的动点的轨迹为圆。而在现行解析几何的坐标中，任意两点都对应两个数或者两个数组，也就是说，任意两个点或两个数之间都可以插入无限多个点或者数（数组），只有这样，几何图形或区间才有长度（测度）可言。基于此，不管边数怎样无限增多，正多边形的任意一个边的两个端点都不会重合，只有这样，正多边形才保有周长。然而，这样一来，“到定点的距离为定长的动点的轨迹”反倒不存在了，而有的只是边长无限小下去的动态正多边形。极限论的来源就是“正多边形边数无限增多的极限是圆”，而在现行实数理论体系之下的解析几何中，极限论中的极限都不存在了，尤其是瞬时变化率对应的切线和积分对应的曲边梯形不存在了，而展现在解析几何中的只能是切割长度无限减小的割线和折数无限增多的折线梯形，切线和曲边梯形反倒不存在。解析几何是数与形的统一，也就是说，现行实数系下的解析几何从数和形两个方面否定了极限论。难道维尔斯特拉斯的以ε-δ语言表达的极限原理就可以超越现行数学的数-形模型吗？

一句话，极限论建立的前提是想当然的，而这种“想当然”是不存在的。

以想当然而实际上仍然无法自圆其说的极限论为依托的柯西的微积分原理怎么自圆其说？再看现行微积分原理的微分定义：

现行微积分原理定义微分的方式无非如下三大类：

对于这三种做法人们不免要问：

 2. 微分的过渡性讲法

建立并让数学教师们习惯新的数学的数-形模型，还需要时日，因为这本质上是一场数学革命。然而，我们可以先搞一个过渡性的微分定义。

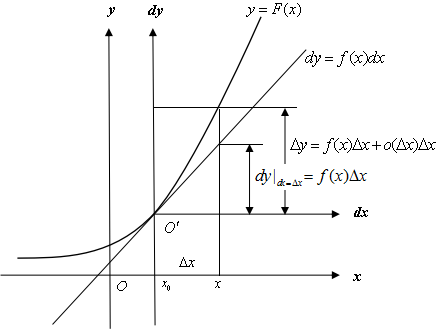
这里的微分定义与传统的微分定义的一个根本的不同在于，dx与△x以及dy与△y不再有必然联系。对于多元微分，定义方式还是这样。这样一来，微分不再自相矛盾，隐函数的导数、参数方程的导数和不定积分的第二类换元法，以及微分方程求解原理也都不再说不通。                                                    

3. 结论

如上定义微分的办法，虽然不再导致微积分原理自相矛盾，但是，如果从细微处着眼，仍然存在不够严密的问题。因此，这个办法只能权作下一次数学革命前的过渡性办法。

（声明：本文仅代表作者观点，不代表本站观点，仅做陈列之用）

[责编：tdsr]

郑重声明：本文版权归原作者所有，转载文章仅为传播更多信息之目的，如作者信息标记有误，请第一时间联系我们修改或删除，多谢。