摘要: 围绕微积分基础理论问题,学术界展开了广泛的讨论。尤其是丁小平的《浅谈现行微积分原理的错误》、《略论作为微积分原理的完善的实变函数》和《微分之讲授》等系列文章发表以后,引起了很大的学术争议,有学者发文为现行微积分体系辩护。本文对其中有关微分概念的问题进行评析和探讨,指出现行的微积分原理体系确实存在逻辑错误,有必要对其进行重新思考。
Abstract:Around the basic theoretical issues about the calculus, scholars launched a wide-ranging discussion. In particular, Ding Xiaoping’s articles “A Brief Discussion on Mistakes in Current Principle of Calculus”, “A Brief Discussion on the Functions of Real Variables as the Perfection of Principle of Calculus” and “How to Teach Differential Correctly” have caused great academic controversy. Some scholars issued academic papers to defend the current calculus system. This paper discusses the problem on the concept of differential, pointing out that logic errors do exist in the current calculus principle system, and it is necessary to rethink it.
Keywords:Calculus Principle; Derivative; Differential; Differential Quotient
1. 引言
长期以来有关微积分理论问题的讨论从未中断过。2012年,师教民在《高等数学研究》发表《论极限理论的微分之谜》 [1] 。以这篇文章为标志,数学界围绕微积分基础开展了广泛的讨论,其中既有如徐利治老师、张景中院士这样的学界泰斗,也有青年学者如徐嘉、张乔等。
在此期间,丁小平发表了系列文章,深入探讨了相关问题。2015年,丁小平在《前沿科学》杂志第4期发表了《浅谈现行微积分原理的错误》 [2] 一文,系统地指出现行微积分原理中存在的错误。基于大家公认勒贝格等人关于实变函数理论的工作完善了微积分原理这一情况,丁小平在2016年《前沿科学》第4期上发表了《略论作为微积分原理的完善的实变函数》 [3] 一文,指出实变函数理论中的一些严重错误,以此来论证实变函数理论并不能证明现行微积分原理是正确的。考虑到现行微积分的教学需要,丁小平随后在2017年《前沿科学》第3期上又发表了《微分之讲授》 [4] 一文,给出了不存在逻辑错误的微分定义,以便于新的微积分没有出来之前的过渡性教学。
2018年,曾志强等对这次论战进行了总结,并在《高等数学研究》2018年第5期上发表了《综述<论极限理论的微分之谜>引发的论战》 [5] (以下简称《综述》)一文,认为第二代微积分仍然存在问题,回避了第一代微积分中微分的逻辑错误问题,该文含蓄地支持了丁小平的观点。
另一方面,更多人反对丁小平的观点,但大多属于脱离数学的辩驳和攻击,仅有极少数学者从数学科学的角度,按照一定科学规则对丁小平的学术观点进行批驳。其中科学网《数学啄木鸟专栏》 [6] (以下称“专栏”)对在《科学出版社》、《上海交通大学出版社》出版的专著和一些期刊、学报上发表的文章进行了认真的探讨。近期有学者在该专栏发表了系列针对上述质疑微积分理论问题的文章,其科学态度值得敬佩,观点也较具代表性。
笔者认为提出一个充满争议的学术观点是一件难得的事情,故本文就专栏《这是不同的微分变量——兼评丁先生的错误论点》等相关文章的主要观点展开深入的探讨,并希望通过系统地分析各方学术观点,进一步清楚阐释微积分原理体系确实存在逻辑错误。
2. 丁小平与批评者在现行微积分原理上的见解
为了便于理解上述争论,试以复合函数为例,简要说明丁小平和专栏评述文章对此问题的看法。
2.1. 丁小平关于微分的批判
现行数学分析经典教材通常将微分定义为函数增量的线性主部。考虑复合函数 y=F(x) , x=G(t) ,有

显然,可知 dx≠Δx 。进而,从复合函数出发得到了存在差异的 dx和dy ,即从微分定义出发得出了矛盾的结论,故而现行微分定义是错误的。
上述论证过程是丁小平文中提及的过程。事实上,除了可以通过复合函数推导微分错误外,其还提供了积分换元法、常微分方程、隐函数、多元微分等其他途径的论证途径,详细论证具体参见其发表论文,在此不一一赘述。
2.2. 批评者的观点
为了批驳丁小平的观点,《数学啄木鸟专栏》中曾针对丁小平在《前沿科学》发表的三篇文章,发表了《这是不同的微分变量——兼评丁先生的错误论点》一文 [7] ,提出了三点批评意见:1) 对于同一个变量y,将其看作不同函数关系中的因变量时,其微分 dy 也不同;2) 不同场合下不同公式中的 dx 可能不是一个变量;3) “微分的形式不变性”不是“相等微分变量的替换”。他认为上节论证过程矛盾的原因仅在于由不同路径得出的 dx 是不同的东西,一个是自变量的微分,一个是因变量的微分。
作者认为:“一般说,通常用一个符号(名称)表示一个东西,这没错。但是不能绝对化……要知道有些时候,‘在明确的条件下,一个符号(名称)完全可以表示不同对象’。”“因为这里是用的 dx=Δx 的微分变量 dx ,与 dx≠Δx 的微分变量 dx 不是同一个 dx 。前者是自变量的微分 dx ;后者是因变量的微分 dx 。”于是,“丁小平先生在文中所说的‘微积分的错误’,根本就不是什么错误而是对‘微分’概念的误读……,一旦纠正了这些错误的解读,那些对微积分原理的质疑就会顿时烟消云散,化为乌有。”
3. 对批评者观点的探讨
3.1. 对批评者论证过程的评析
微分定义在微积分体系中占据着重要的和基础的位置,故有必要对微分的概念进行认真的辨析。另外,需要说明的是,在人类历史上,微积分方法的发明先于其理论基础的发现,因此对理论和原理的探讨并不影响微积分方法的的适用性和有效性。
在第二代微积分原理中,微分的定义主要包括两部分,因变量的微分定义为函数增量的线性主部 [8] [9] ,即 dy=f(x)Δx ;自变量的微分定义为自变量的增量,或使用恒等函数 y=x 或 x=x ,得到 dx=Δx ,从而得到 dy=f(x)Δx 的形式,进一步得到微商的表达式

换一个角度看,如果定义 dx 是自变量x微分,那么, f(x)=dy/dx 就不适用于 y=F(x) , x=G(t) 的情形;如果定义 dx 是因变量 x=G(t) 的微分,那么, dx 就不是自变量x微分。如果还有人诡辩说,对于 y=F(x) , x=G(t) 的情形,就定义 dt=Δt ,那么,我们说 y=F(x) 就不再能写成微商 f(x)=dy/dx 的形式。
按照该学者的观点, dx 只是一个记号,在不同情形下表达不同的含义。即便从显式表达的函数出发,可以清晰地辨识符号 dx 所表达的含义;那么在第二类换元法积分过程中,如何判断 dx 的含义呢?例如
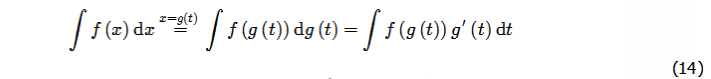
这里涉及到dx究竟是y=f(x)的“自变量x的微分”,还是后者是“函数x=g(t)在t0点的微分”?事实上,如果此dx非彼dx,那么在任何涉及到复合函数的微分方程求解过程,都是自相矛盾的,比如隐函数求导、参数方程求导。
3.2. 微分定义的过渡性讲法
批评者如认真读过丁小平《微分之讲授》 [4] 一文,也许不会出现上述误解,因为该文给出了无逻辑矛盾的微分定义方式(当然,作者也明确提到这只是微积分原理的过渡性讲授方式),诚如任何一位逻辑不混乱的人所知,在确定的前提下,两个相矛盾的命题不能同时真。“ 。A和非A必有一真,不可能既不是A,又不是非A。” [10] 。
《微分之讲授》采用如下方式定义微分:

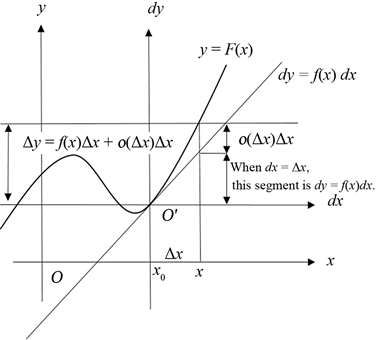
Figure 1. A sketch map of the definition of differential
图1. 微分定义示意图
按照这种定义方式易知,当dx=Δx时,dy=f(x)dx=f(x)Δx就是Δy的线性主部,即Δy-dy=o(Δx)dx。显然,导函数f(x)可以表示为微商dy/dx的形式。
仔细分析,可知《微分之讲授》中微分定义与传统微分定义的存在根本的不同,即dx与Δx以及dy与Δy不再有必然的联系。同时,这种定义方式也适用于多元微分的定义。这样,微分不再自相矛盾,对于隐函数的导数、参数方程的导数和不定积分的第二类换元法,以及微分方程求解原理均可给出逻辑自冾的表述。
如果丁小平提出的新微分定义是持之有故言之成理的,那么,批评者所说的“一个符号(名称)完全可以表示不同对象”观点的对与错也就一目了然了。
4. 结束语
事实上,关于微分错误的讨论一直存在。南京大学数学家莫绍揆曾发表《试论微分的本质》 [11] 一文,该文深刻批判了现代体系中由于强行引入微分的概念,而使得必须有dx=Δx的做法。并指出在多元微分学中可以取消微分的定义,但是考虑到微分在积分学、微分几何等地方的应用,提出取消自变量微分的定义,而保留因变量微分的定义。除此之外,米哈列·列夫索次院士 [12] ,林群院士,张景中院士都认为现代的微分引入极限以后显得过于繁琐,提出不需要极限概念直接、自然却严格地建立微分和积分理论的新方法。最近林群院士和张景中院士在《高等数学研究》上发表文章 [13] ,依据“平均速度一定夹在两个瞬时速度之间”的思想,通过建立差商不等式,建立了不用极限的导数理论,从而建立了一个微积分体系。
微分概念是现行微积分体系的基础,然而微分定义却存在不可回避的逻辑矛盾。同时,现实世界和微积分方法中都需要解释瞬时变化率,而不管极限论还是截止目前为止的微商定义都没解决瞬时比的数学表达问题,因此,都是不合格的微积分原理。这种矛盾绝不像有些现行体系拥护者所解释的是“同一符号表示的不同对象”,而是由于现有的数形模型存在的缺陷导致的。本文介绍了丁小平提出的过渡性质的新的微分定义,如果在柯西意义上说新微分定义不再存在逻辑矛盾,那么也就从反面说明柯西意义的微积分原理和试批者的反驳都是站不住脚的。在此基础上,丁小平曾在新的数形模型的基础上构建了完全满足微积分方法要求的微积分原理。笔者有幸聆听过的他的讲座,这个新的微积分原理以立论的形式再次反衬了现行微积分原理的不足。
科学应该容许质疑和讨论,经典教材的说法也并非逻辑完备无可指摘,只要这种质疑和讨论秉持持之有故言之成理的准则。因为,“有条件的怀疑是科学精神”的基本内涵,接受他人的批判,批判他人的成果,是科研工作者的权利和义务。
文章引用:
赵雪婷. 微分概念问题再探讨[J]. 理论数学, 2019, 9(5): 621-626. https://doi.org/10.12677/PM.2019.95082

(声明:本文仅代表作者观点,不代表本站观点,仅做陈列之用)
[责编:tdsr]
郑重声明:本文版权归原作者所有,转载文章仅为传播更多信息之目的,如作者信息标记有误,请第一时间联系我们修改或删除,多谢。



tdsrwz@163.com
